Riley's tree cricket

Oecanthus rileyi

Thermometer Crickets

Chirps Rates of Species in the O. rileyi Species Group
Relative to Temperature (°C)

Trend lines for 4 species in the O. rileyi group. Figure 3, from Walker and Collins 2010.

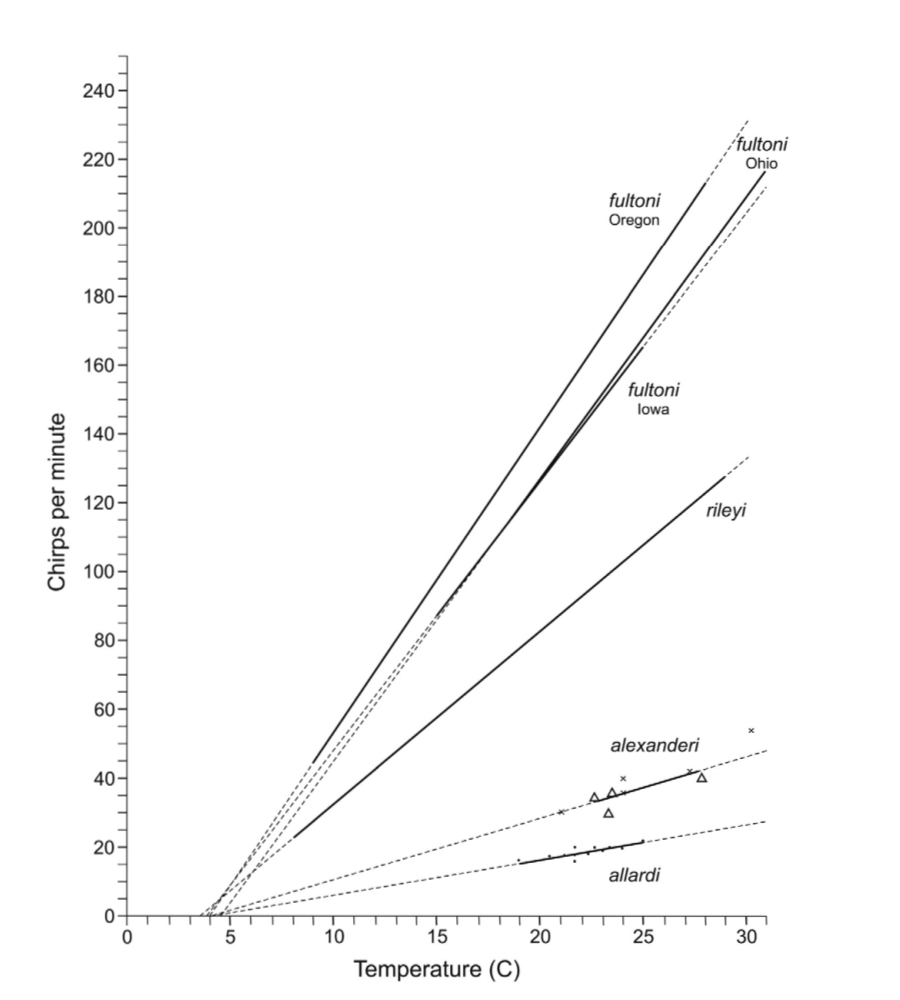
Species within the Oecanthus rileyi group have calling songs composed of chirps or brief trills that are easily countable and exhibit highly regular rates that vary linearly with temperature. The above graph shows the trend lines for O. fultoni (Oregon, Ohio, and Iowa), O. rileyi, O. alexanderi, and O. allardi. Solid portions of the lines represent data points; dotted lines indicate extrapolated values. The extrapolated regression lines tend to converge at 4 °C, where the chirp rate is expected to be zero. Based on this relationship, simple formulas can be calculated that convert chirp counts into highly accurate estimates of ambient temperature. The formula provides a time interval (in seconds) for counting the number of chirps heard from a singing cricket, which is then added to a number that offsets the temperature range where y = 0.

The formulas for °C and °F for O. rileyi are:

Number of chirps counted in 11 seconds + 4 = temperature °C

Number of chirps counted in 20 seconds + 39 = temperature °F

NOTE: Graphs shown on this web page and data used for making calculations are from Walker and Collins (2010) and its supplemental content.

How to Calculate Tree Cricket Temperature Formulas

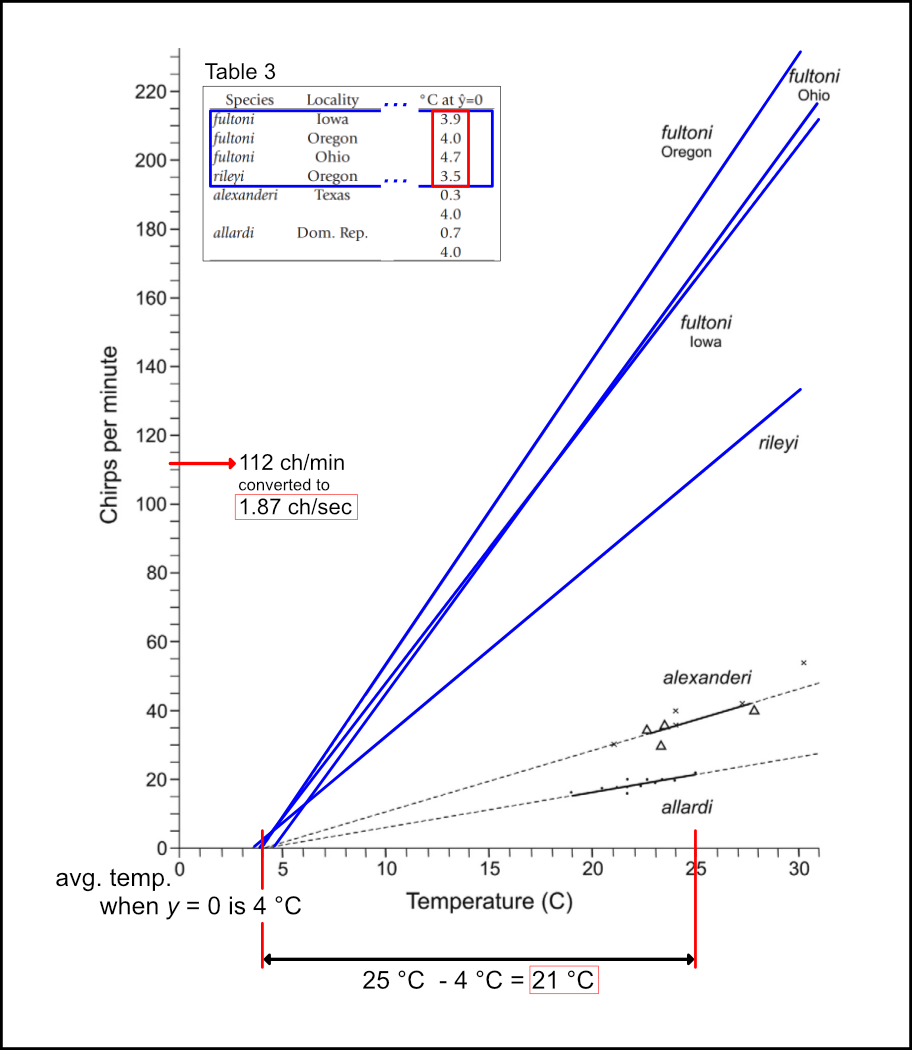
Here is an example using a data set for O. rileyi with 112 chirps per minute at 25 °C (77 °F).

The time interval for counting chirps is equal to the reciprocal of the slope for a given species. Because the count time is given in seconds (which provides a practical measurement), the chirp rate should be expressed in seconds. Therefore, the first step is to convert chirps per minute to chirps per second. For our example:

chirps/second =

112 chirps

1 minute

60 seconds

1.87 chirps

second

The number of chirps per second represents the numerator of the slope. The denominator is the span of degrees in relation to the number of chirps per second.

Figure 3 from Walker and Collins (2010). Modifications on this graph include: changing regression lines for O. fultoni (Iowa, Oregon, and Ohio) and O. rileyi from black to blue; inserting columns 1, 3, and 7 from Table 3 (Walker and Collins 2010); inserting red arrow to note conversion from chirps per minute to chirps per second; noting average temperature for °C when y = 0; and adding red vertical lines and black line with double-headed black arrows to show degree span for chirp rate at 25 °C.

The denominator of the slope is the span of degrees between the temperature where y = 0 and the temperature associated with the chirp rate being considered (1.87 chirps per second at 25 °C). The temperature at y = 0 that is used in the formula is the average of the four blue regression lines shown in the above graph. These lines are for O. fultoni (Iowa, Oregon, and Ohio) and O. rileyi and the average temperature is 4 °C (39 °F). The degree span is calculated by subtracting the temperature at y = 0 from the upper temperature.

For °Celsius:

degree span =

25 °C - 4 °C = 21 °C

For °Fahrenheit:

degree span =

77 °F - 39 °F = 38 °F

To determine the slope of the regression line, divide the chirp rate by the degree span.

For °Celsius:

slope =

1.87 chirps/second

21 °C

0.089 chirps/second

1 °C

For °Fahrenheit:

slope =

1.87 chirps/second

38 °F

0.049 chirps/second

1 °F

The count time is the reciprocal of the slope.

For °Celsius:

reciprocal of slope =

0.089

11.2 seconds

For °Fahrenheit:

reciprocal of slope =

0.049

20.4 seconds

Add the average temperature when y = 0 (which was subtracted when calculating the degree span) to the count time to get the estimated temperature. These are the final formulas:

Number of chirps counted in 11 seconds + 4 = temperature °C

Number of chirps counted in 20 seconds + 39 = temperature °F

NOTE: Using all paired data sets for O. rileyi, the average count time in °C is ≈ 11 seconds and for °F is ≈ 20 seconds. Data used for calculating these averages can be found in the supplemental content for Walker and Collins (2010).

Example

Below is an audio file of O. rileyi singing for 11 seconds. Count the number of chirps.

There are 15 chirps. Use the formula to calculate temperature in °C.

15 chirps + 4 = 19 °C

Is this correct?

Convert the chirps per second to chirps per minute and compare the results to the graph showing the trend line for O. rileyi.

chirps/minute =

15 chirps

11 seconds

60 seconds

1 minute

81.8 chirps

minute

On the graph for O. rileyi, draw a vertical line from 19 °C on the x-axis to meet the trend line. Then draw a horizontal line from 81.8 chirps per minute on the y-axis to the trend line. The two lines do not cross exactly on the trend line, but they are close enough to be a good estimate.

Trend line for O. rileyi. Supplemental content from Walker and Collins (2010). Blue lines were added to the graph.

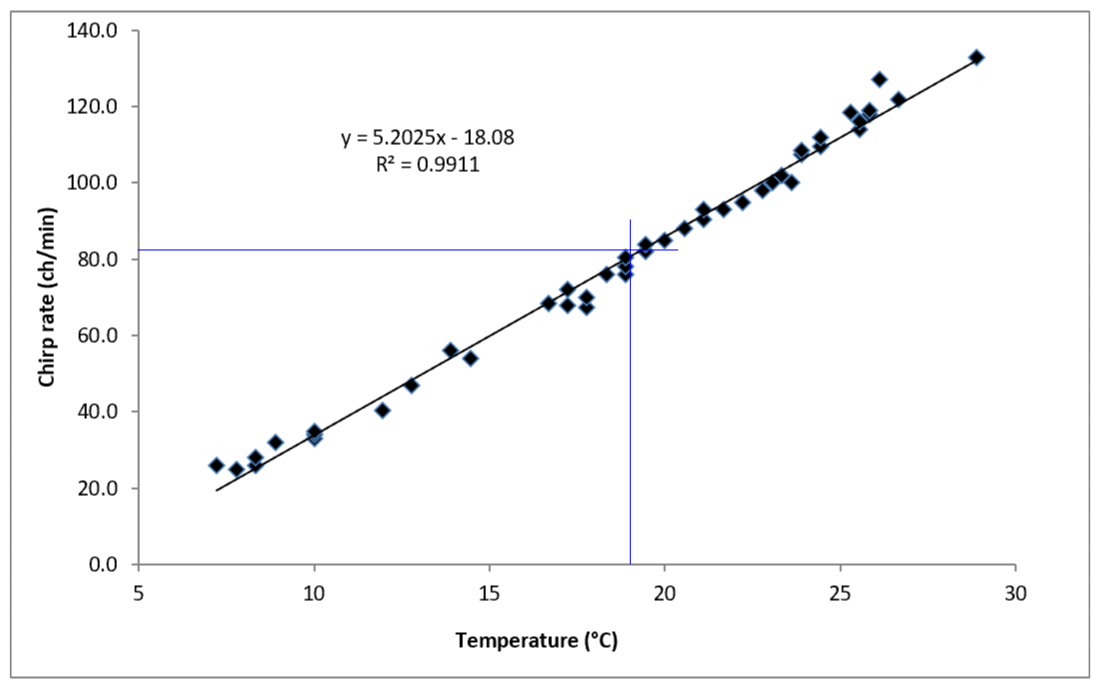
Data points (Walker and Collins 2010, supplemental content) around 19 °C are:

Temperature °C	Chirps/minute
18.89	76.0
18.89	78.0
18.89	80.5
19.44	82.0
19.44	84.0
average chirp rate:	80.1

The song used in this example was recorded by J. Banas in Bernalillo County, New Mexico at the recorded temperature of 19 °C. The audio for this song is on O. rileyi's species page with a duration of 16 seconds. The audio was trimmed to 11 seconds for this example. The graph, data, and field measurements align with the temperature calculated using the tree cricket formula for estimating temperature based on chirp rate. Therefore, we can conclude that the temperature calculated using the formula is a good approximation of the actual temperature.